ここでは鏡映変換
\[
Q(\theta) = \left(
\begin{array}{cc}
\cos(2\theta) & \sin(2\theta) \\
\sin(2\theta) & -\cos(2\theta)
\end{array}
\right)
\]
について考えます。
まず、モータ制御をするにあたって、次のような性質がある行列が分かると便利です。
「α,β平面にある任意の点xを、”角度θを対称とする角度かつ、原点からの距離がxと同じ”点に映す。」
何言ってるかわからないので、下の図を見てください。
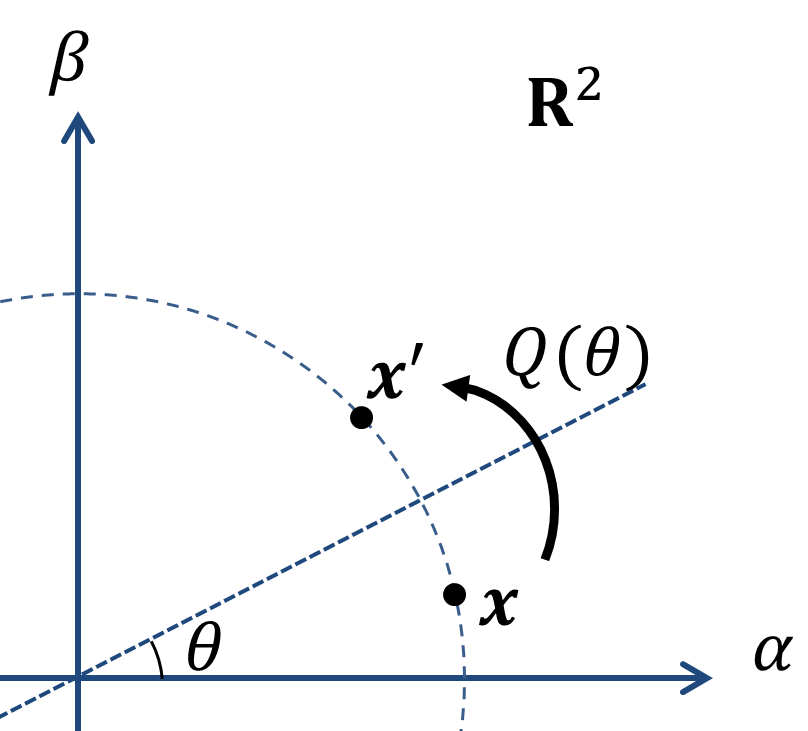
はい、これを考えていきます。
考えるにあたり、変換を次のように解釈すれば容易です。
①回転行列をかけて補助線0度にする。
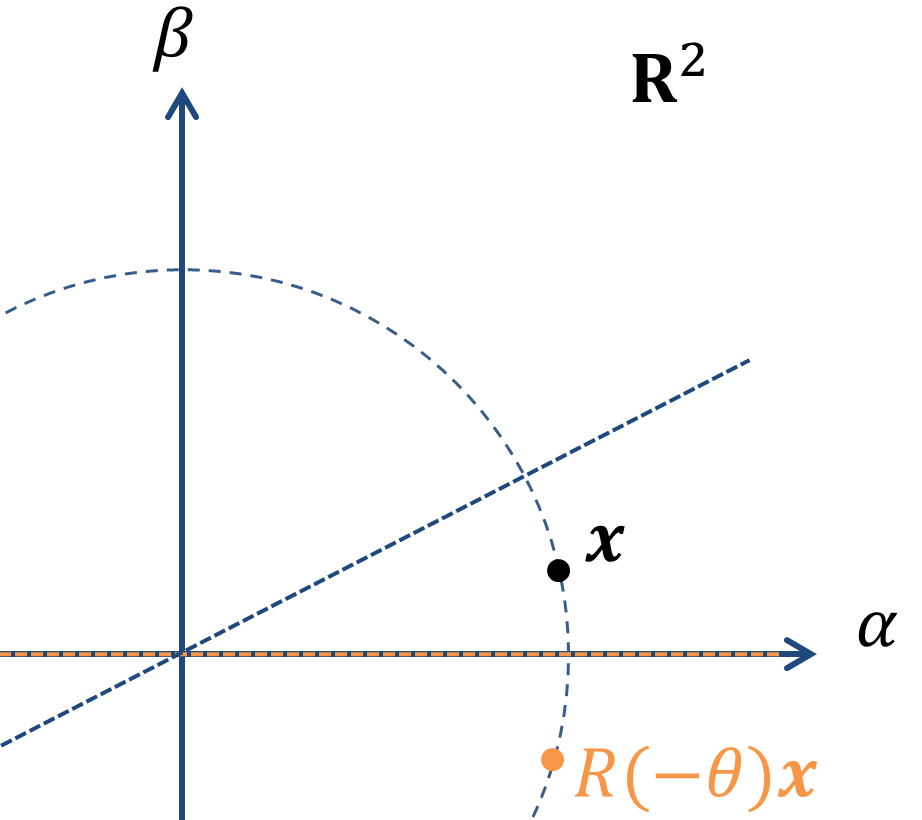
②0度を中心の鏡映変換を考えてあげる(ここではTとします。)
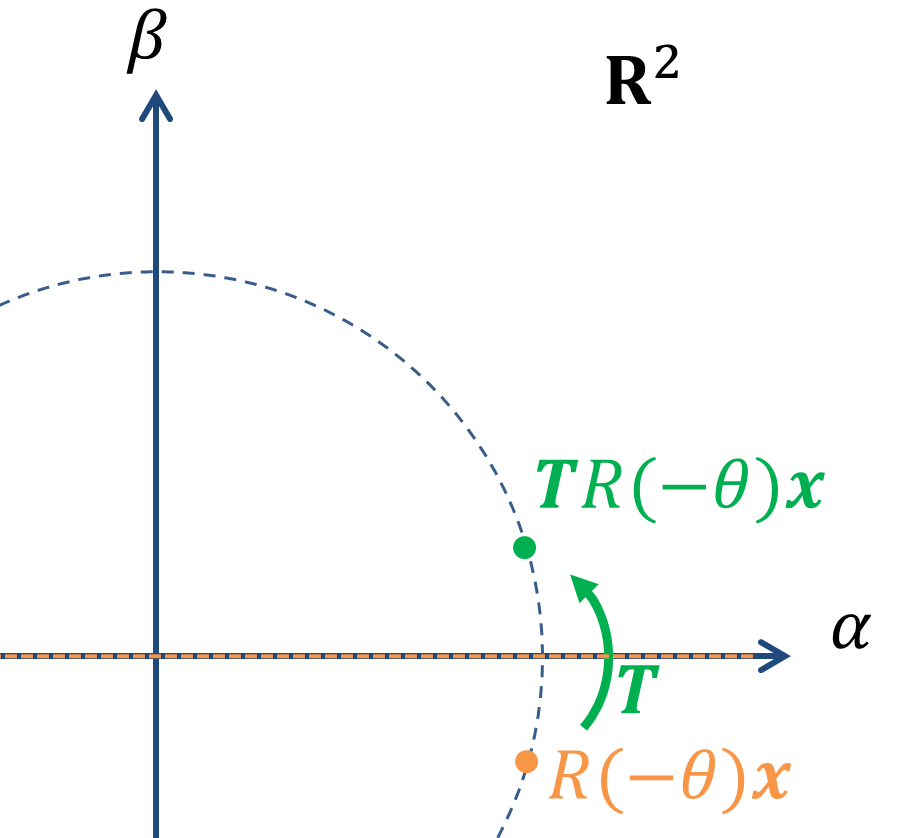
③補助線をもとの角度θに戻す。
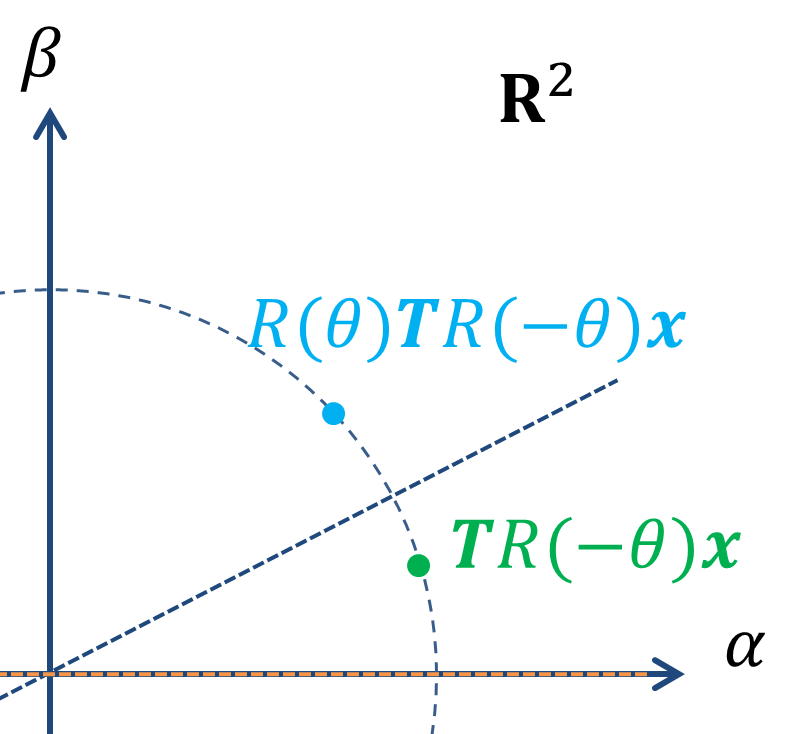
この操作をすることで、
\[Q(\theta)=R(\theta)TR(-\theta)\]
という行列に変換できます。
(結局Tで鏡映変換しているので、面倒くさくしてるだけじゃん!)と思われると思いますが、0度の鏡映変換は、β(y座標)を反転させるだけなので、極めて簡単な行列で表現できます。
\[
T =
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
\]
これを使って以下のように計算できます。
\[
R(\theta)TR(-\theta)
\]
\[
= \begin{pmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
\begin{pmatrix}
\cos\theta & \sin\theta \\
-\sin\theta & \cos\theta
\end{pmatrix}
\]
\[
=\begin{pmatrix}
\cos^2 \theta – \sin^2 \theta & 2\sin\theta \cos\theta \\
2\sin\theta \cos\theta & -\cos^2 \theta + \sin^2 \theta
\end{pmatrix}
\]
\[
=\begin{pmatrix}
\cos(2\theta) & \sin(2\theta) \\
\sin(2\theta) & -\cos(2\theta)
\end{pmatrix}
\]
\[
=Q(\theta)
\]
つまり、θを対称とする鏡映変換は、このような2θの三角関数の行列で表現できる訳です。面白いですね。